GRE Math : Lines and Angles

GRE Math : Lines and Angles

Plane geometry is devoted primarily to the properties and relations of plane figures, such as angles, triangles, other polygons, and circles. The terms “point”, “line”, and “plane” are familiar intuitive concepts. A point has no size and is the simplest geometric figure. All geometric figures consist of points. A line is understood to be a straight line that extends in both directions without end. A plane can be thought of as a floor or a tabletop, except that a plane extends in all directions without end and has no thickness.

Given any two points on a line, a line segment is the part of the line that contains the two points and all the points between them. The two points are called endpoints. Line segments that have equal lengths are called congruent line segments. The point that divides a line segment into two congruent line segments is called the midpoint of the line segment.

In Geometry Figure below, A, B, C, and D are points on line l;

Line segment AB consists of points A and B and all the points on the line between A and B. According to Geometry Figure 1 above, the lengths of line segments AB, BC, and CD are 8, 6, and 6, respectively. Hence, line segments BC and CD are congruent. Since C is halfway between B and D, point C is the midpoint of line segment BD.

Sometimes the notation AB denotes line segment AB, and sometimes it denotes the length of line segment AB. The meaning of the notation can be determined from the context.

When two lines intersect at a point, they form four angles. Each angle has a vertex at the point of intersection of the two lines. For example, in Geometry Figure 2 below, lines L1 and L2 intersect at point P, forming the four angles APC, CPB, BPD, and DPA.

The first and the third of the angles, that is, angles APC and BPD, are called opposite angles, also known as vertical angles. The second and fourth of the angles, that is angles CPB and DPA are also opposite angles. Opposite angles have equal measures, and angles that have equal measures are called congruent angles. Hence, opposite angles are congruent. The sum of the measures of the four angles is 360º.

Sometimes the angle symbol  is used instead of the word “angle”. For example, angle APC can be written as APC

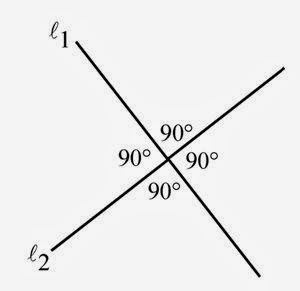
Two lines that intersect to form four congruent angles are called perpendicular lines. Each of the four angles has a measure of 90º. An angle with a measure of 90º is called a right angle. Geometry Figure 3 below shows two lines, L1, L2 that are perpendicular, denoted by L1 L2

A common way to indicate that an angle is a right angle is to draw a small square at the vertex of the angle, as shown in Geometry Figure 4 below, where P O N is a right angle.

An angle with measure less than 90º is called an acute angle, and an angle with measure between 90º and 180º is called an obtuse angle.

Two lines in the same plane that do not intersect are called parallel lines. Geometry Figure 5 below shows two lines L1 & L2 that are parallel, denoted by  L1L2 . . The two lines are intersected by a third line, L3 forming eight angles.

Note that four of the eight angles in Geometry Figure 5 have the measure xº, and the remaining four angles have the measure yº, where x + y = 180.

Learn Lines and Angles Basics